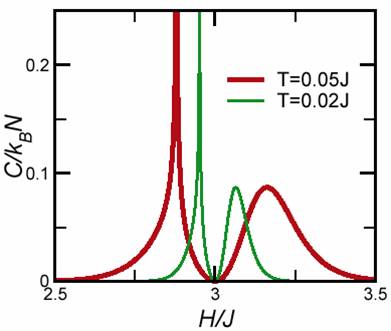
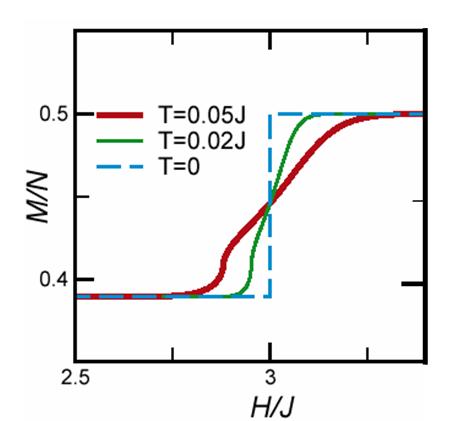
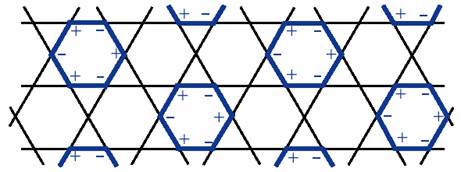
マグノンは磁性体において磁気励起を担っているボゾンです。磁場を変化させた時の磁化曲線に現れる磁化プラトーは、マグノンが結晶を作っている状態として理解することができます。マグノンの濃度が特定の値の時には、マグノンが実空間で周期的で特殊なパターンを作って局在化するため、その前後の濃度の時よりもエネルギーが特に安定になるからです。しかしながらエネルギーをマグノン濃度や温度の関数として正確に計算することは、複雑な多体問題を解く必要があるため通常非常に困難です。

　我々はフラストレートした量子スピン系の飽和磁場近傍のエネルギーをほぼ厳密に計算することに成功しました。特に、1次元の鋸歯格子と2次元のカゴメ格子上のスピン1/2の場合を中心に研究を行いました。フラストレートした格子の特徴はエネルギーの分散関係が全くないフラットなマグノンモードが存在することで、このことは強磁場の元でマグノンが有限領域に閉じこめられて運動していることを意味しています。この広がったマグノン同士の相互作用は元の格子と双対な関係にある格子上の近接相互作用を持つイジング模型として記述できます。この模型の低温極限のエネルギーを漸近的に厳密に計算しました。

　この結果を用いて、カゴメ格子の場合には有限温度で並進対称性の破れに対応する相転移が有限温度で現れ、これが7/9プラトーに対応することを示しました。また、この転移が3状態ポッツ模型の普遍クラスに属することを証明することができました。